Simples aplicação de Mínimos quadráticos

Motivação!

A motivação para essa aplicação surgiu após ver o tema do dia 09/01/2024 do TidyTuesday!

Basicamente, se trata de fazer uma análise de um data base para responder a seguinte pergunda: “As datas de nascimento ainda são um destino para os jogadores canadenses da NHL?”, tema bastante discutido no link!

Os dados foram coletados do Statistics Canada, NHL team list endpoint e NHL API

Análise

Para ter uma ideia do banco de dados:

A análise que irá ser feita, usará apenas a coluna birth_month que representa o mês de nascimento do jogador!

Como queremos transformar esses dados em formato de matriz para aplicar técnicas da Álgebra Linear vamos entender esse data base como uma matriz:

$$\left(\begin{array}{cc} x & y \\ 1 & 876 \\ 2 & 819 \\ 3 & 834 \\ 4 & 796 \\ 5 & 783 \\ 6 & 692 \\ 7 & 696 \\ 8 & 602 \\ 9 & 639 \\ 10 & 620 \\ 11 & 561 \\ 12 & 556 \\ \end{array}\right) = A = \left(\begin{array}{cc} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \\ 1 & 6 \\ 1 & 7 \\ 1 & 8 \\ 1 & 9 \\ 1 & 10 \\ 1 & 11 \\ 1 & 12 \\ \end{array}\right),B = \left(\begin{array}{c} 876 \\ 819 \\ 834 \\ 796 \\ 783 \\ 692 \\ 696 \\ 602 \\ 639 \\ 620 \\ 561 \\ 556 \\ \end{array}\right)$$

Conforme visto em Ortogonalidade e Mínimos quadráticos:

$$\text{Vamos usar a fórmula: }proj_{col A}b = (A^{t}A)x=A^{t}b$$

$$A^{t}A = \left(\begin{array}{cc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \end{array}\right) \left(\begin{array}{cc} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \\ 1 & 6 \\ 1 & 7 \\ 1 & 8 \\ 1 & 9 \\ 1 & 10 \\ 1 & 11 \\ 1 & 12 \\ \end{array}\right) = \left(\begin{array}{cc} 12 & 78 \\ 78 & 650 \\ \end{array}\right)$$

Temos ainda que:

$$A^{t}b = \left(\begin{array}{cc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \end{array}\right) \left(\begin{array}{c} 876 \\ 819 \\ 834 \\ 796 \\ 783 \\ 692 \\ 696 \\ 602 \\ 639 \\ 620 \\ 561 \\ 556 \\ \end{array}\right) = \left(\begin{array}{c} 8474 \\ 50749 \\ \end{array}\right)$$

Agora escalonamos a matriz:

$$\left(\begin{array}{cc|c} 78 & 650 & 50749 \\ 12 & 78 & 8474 \\ \end{array}\right) = \left(\begin{array}{cc|c} 0 & 1 & -30.29 \\ 1 & 0 & 903.07 \\ \end{array}\right)$$

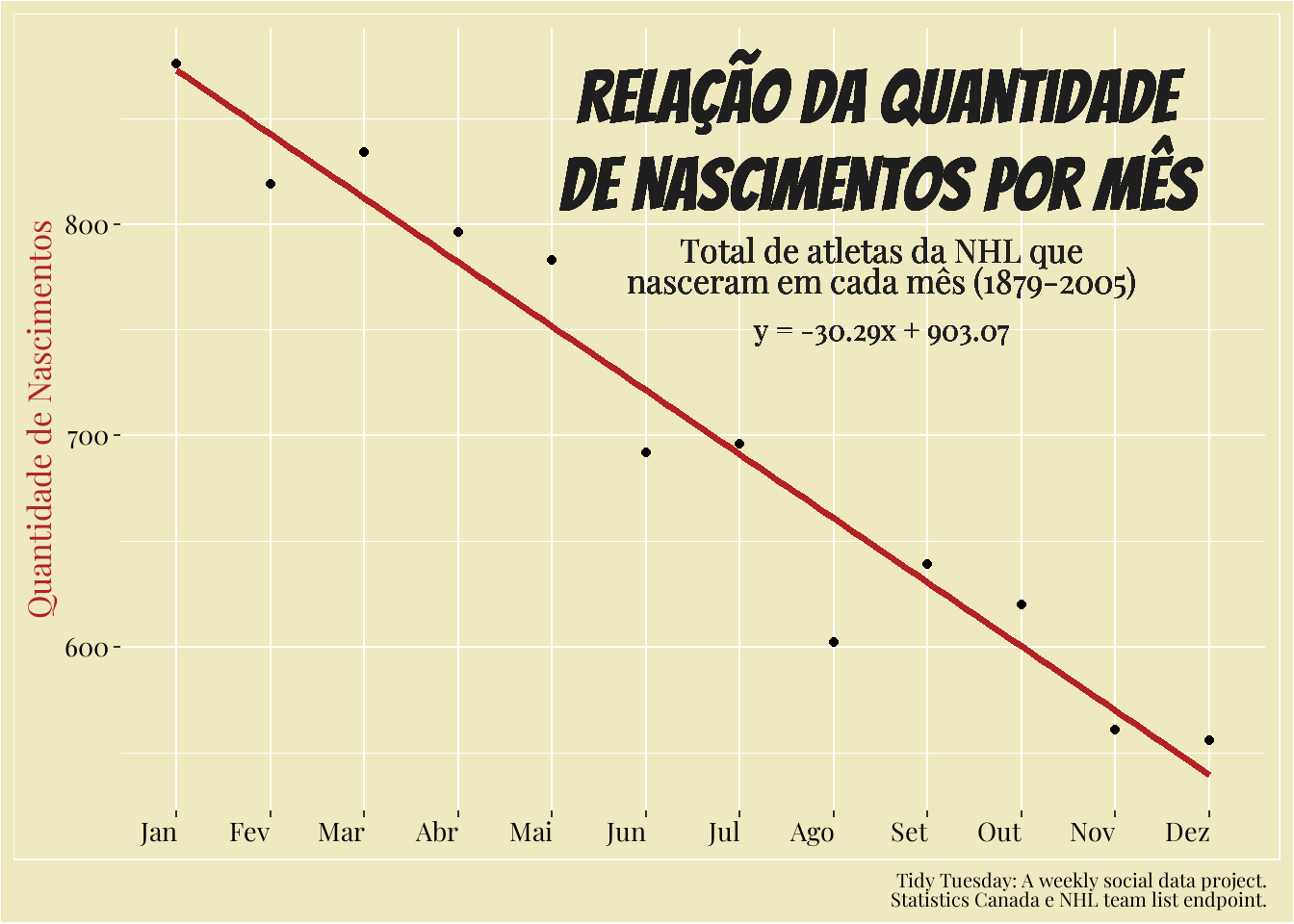
Logo temos a nossa reta y = -30.29x + 903.07